The algorithm used by treeKO to compare trees can be summarized in the following graph:

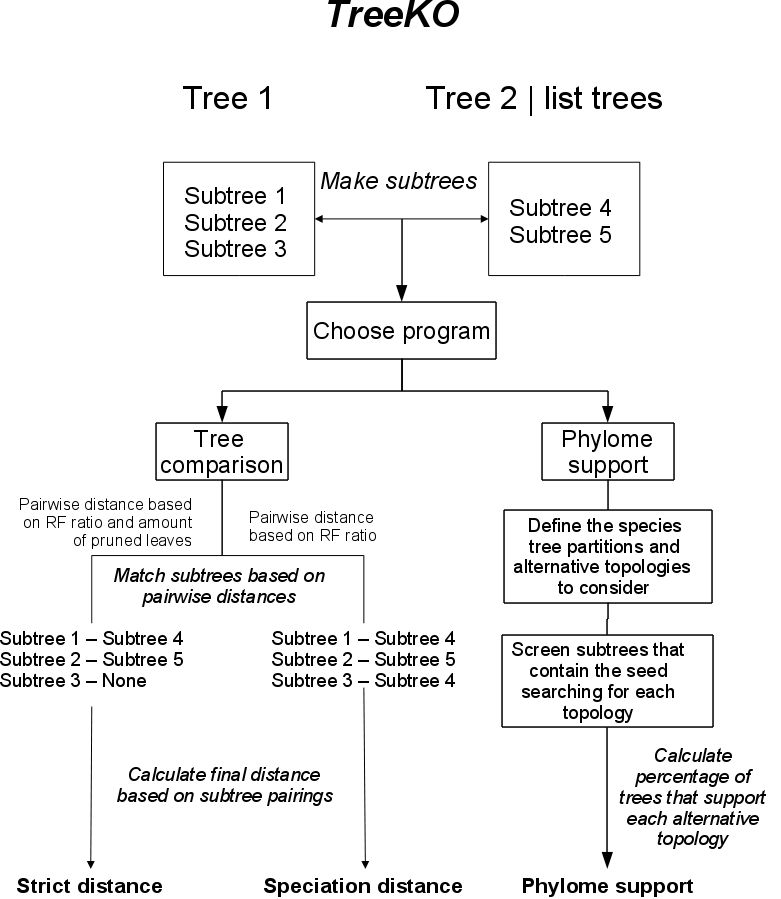
The subtree reconstruction part is common to both programs implemented in treeKO. Depending on the program chosen by the user, treeKO will compare two trees and provide several distance measures. Alternatively treeKO will compute the phylome support for a given species tree.

TreeKO divides the original trees in single gene pruned trees using the duplication nodes as points in which the tree can be split and re-assembled. ETE (REF) is used to root the tree by one of the methods implemented in treeKO and is used to predict all the duplication nodes present in the tree. TreeKO implements two methods in order to detect duplications nodes: species overlap and tree reconciliation. The user can also provide their own duplication annotations using the extended newick format. Then, for each duplication node, the tree is split in three parts: the main backbone of the tree and the two sister clades that from the duplication node. Trees are reassembled combining the tree backbone with one of the sister clades for each duplication node as seen in the figure.

All the possible combinations of duplicated sister clades are taken into account.

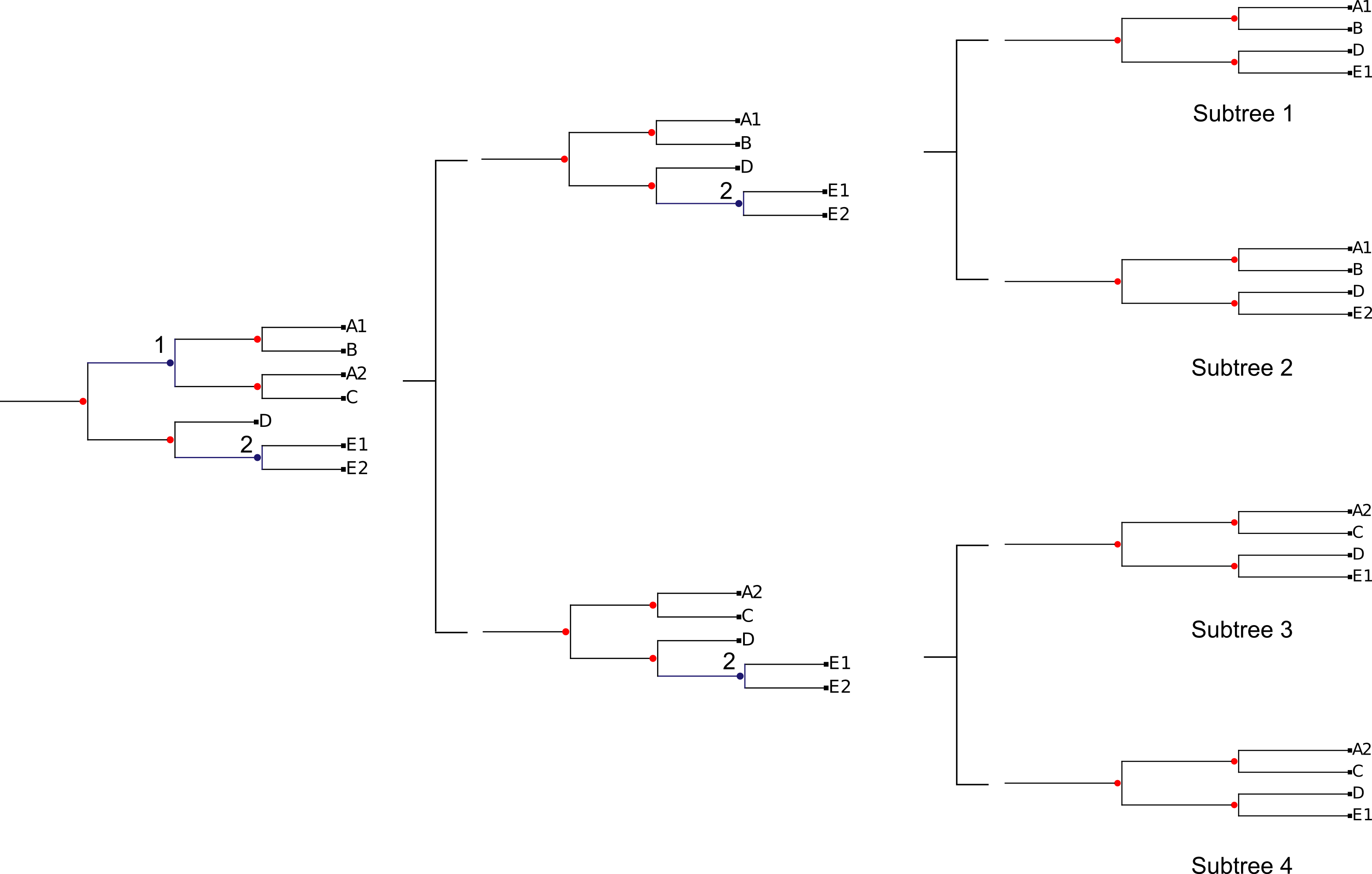
This implies that in trees with a large number of independent duplications the number of pruned trees may increase rapidly. In trees where the species information is available, trees will first be filtered in order to remove intraspecific duplications and therefore lower the number of pruned trees. Pruned trees that have less than three species will take the form of a string and will also be used for the final distance computation.

Horizontal gene transfers

While treeKO is not intended for the detection of horizontal gene transfers (HGT) in phylogenetic trees, a special provision has been implemented when the user supplies information about these events. If the user provides a tree in which HGT events have been marked at the nodes as explained in the |Input files section, then treeKO will first split the tree into pruned tree dividing it by each node marked as a HGT. Independent treeKO calculations will be run for each pair of trees. If the split results in trees that do not contain at least three leaves, these will be compared using the same approach as explained in the tree comparison section. The final distance will be an average of the weighted distances, weights will be calculated by the percentage of leaves the two pruned trees represent from the total number of leaves in both original trees.

Resolution of Multifurcations

When a multifurcation contains more than one protein per species it is assumed that it has at least one duplication node. In order to resolve these multifurcated nodes, they are split in groups of non-overlapping nodes, this will assume a minimum number of duplications for each multifurcated node.

The list of pruned trees can be obtained from TreeKO and be used for other purposes (see "How to run treeKO").

Once the pruned trees for each input tree have been calculated the tree comparison program is able to compare them and calculate the distance that separates the two trees.

Distances, as calculated by the tree comparison program, are a modification of the Robinson & Foulds (RF) calculation and as such only take topology into account. Branch lengths are not considered for the final distance result. Two different distances can be obtained from the tree comparison program: the strict distance and the speciation distance. Both distances are normalized and go from 0 to 1, where 1 would represent two completely different trees.

The strict distance represents the distance that can be derived between two trees if no exceptions for evolutionary significant events are taken into account. If the distance is 0, the two trees will be identical in terms of topology. For each pair of pruned trees a distance is calculated. Two different situations can emerge when comparing pruned trees. If we compare two trees (both have at least three leaves) they are both pruned so that they have the same leaves. If the resulting pruned trees still have more than three leaves, distance is calculated using a normalized RF. The distance is then corrected to take into account the pruned leaves using the following equation:

RF = Robinson & Foulds distance
Rfmax = Maximum Robinson & Foulds distance
LP = Number of leaves remaining in the pruned tree x 2
PT = Number of pruned leaves of both trees

Pruned_tree_distance = ((RF/RFmax) * LP + PT) / (LP + PT)

The equation takes into account the number of pruned leaves by assigning them the maximum RF distance. If the pruned trees have less than three leaves, the RF/RFmax ration will be considered 0 in the equation above. If no overlap was found between both pruned trees distance will be considered 1. The second situation arises when at one or both pruned trees have less than three leaves. In such cases the tree comparison program will search whether there are overlapping proteins. TreeKO will proceed in the same way as for pruned trees with less than three leaves.

Once all the distances are assigned, the tree comparison program progressively selects the lowest distance between a pair of pruned trees until all the pruned trees are matched. The selection is based in first instance by the lowest distance value, but when one pruned tree is matched to different pruned trees with the same distance, the RF value and the size of the two pruned trees are taken into account so that the RF is as small as possible and the size of the pruned trees is as large as possible. Once a pruned tree is chosen, it can not be used in any other pairing. Unmatched pruned trees will be accounted for in the final distance calculation.

TreeKO uses the chosen pairs of pruned trees and calculates the strict distance using the following equation:

D = distance between pruned trees
SLA = Number of leaves in pruned tree A
SLB = Number of leaves in pruned tree B

Strict distance = (((ƩD*SLA) / ƩSLA) + ((ƩD*SLB) / ƩSLB))/2

Unmatched pruned trees are added only to the appropriate term assuming their individual distance is 1.

The comparison between trees with duplication events and with different species content may cause the strict distance between them to be misleading for some purposes. For example, in a situation in which we compare two trees with different sizes, even if both trees have the same topology for the species they share, the strict distance would not be 0 due to the difference in species content. Following the same example, if one of the trees has a duplication, the duplication itself would influence the strict distance even if the topologies after the duplication event had followed exactly the same evolution. Therefore, we may want to look for congruent trees instead of identical ones. Two congruent trees are those from which you can infer the same evolutionary history for the species forming it in terms of speciation events. The speciation distance calculates the distance between two trees without taking into account duplication and loss events. A speciation distance of 0 means that both trees share the same speciation history for the species they have in common.
The algorithm will match the best pairs of pruned trees without taking into account if a pruned tree is used in more than one pairing. In this case the distance between a pair of pruned trees will be represented by the ratio: RF / RFmax. The best pruned tree will be primarily chosen by this ratio. For pairs with the same ratio, a low RF and large pruned tree size will be favored. The final speciation distance will be calculated in the same way as the strict distance (see above for details).

The strict reconciliation between a gene tree and a species tree is calculated. For each incongruence between the species tree and the gene tree a duplication event is assumed with a subsequent number of losses. Two different distances are offered in this mode: Duplication distance and Reconciliation cost distance. In the first one only duplications are computed. In the second both, duplication and loss events are computed. Loss events are considered as nodes that have been lost during the evolution of the gene tree, not as number of species that have lost a copy of the gene during the evolution.

Take as an example the following trees:

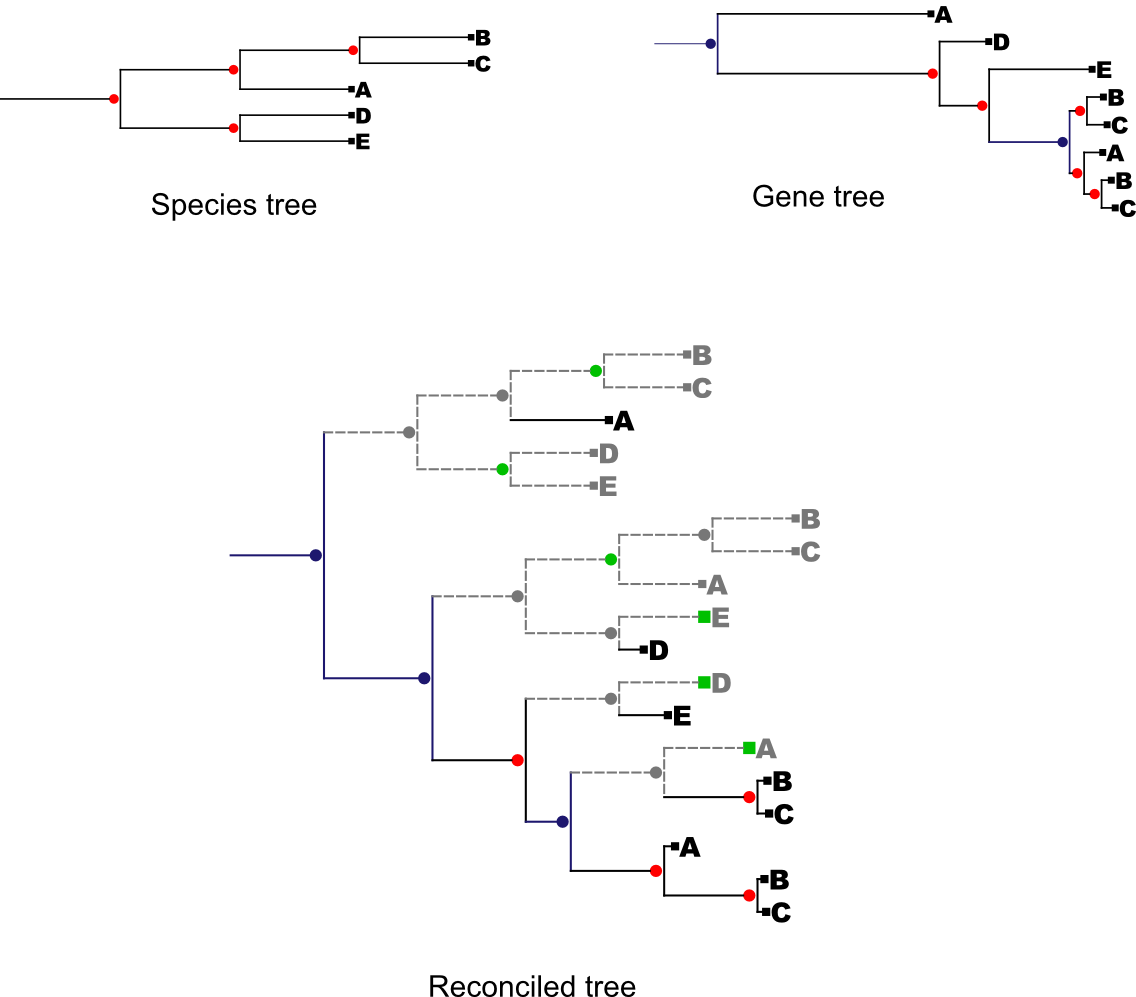
Red nodes : speciation nodes
Blue nodes : Duplication nodes
Green nodes : Lost nodes taken into account in the loss distance
Grey nodes : Lost nodes

In this example the duplication distance would be of 3 and the reconciliation cost distance would be of 9 since there are 6 points in the reconciled tree in which the gene was lost.

The phylome support value for a node can be defined as the percentage of trees in a large collection of gene trees (for instance a phylome) that present exactly the same topological arrangement of the partitions defined by its two daughter nodes.

As seen in the figure, the support for node X will be calculated by searching the number of trees that support the partitions of nodes A,B,C and D (these nodes will be referred as the granddaughter nodes). For a given node, the granddaughter nodes can define three (A,B,C) or four partitions (A,B,C,D) that might display three or fifteen alternative topologies, respectively.

The nodes that are to be considered are read from the species tree. Any node with granddaughters will be considered except for the root of the species tree. Therefore it is important that the user places correctly the root of the species tree.

For each gene tree to be considered for the computation, the pruned trees are calculated. In order to avoid biasing the calculation towards protein families that contain numerous duplications a seed protein needs to be provided for each gene tree. We understand as seed tree the protein or gene from which the tree was constructed. Only those pruned trees that contain the seed tree will be considered.

Each pruned tree will then be searched for the alternative topologies. Pruned trees that do not have at least one species from each of the granddaughters involved in the topology will not be considered, because they do not provide information on that topology.

The phylome support value for a given node will be the result of dividing the number of trees that support the topology found in the species tree and the total number of trees that supported any of the alternative topologies for that node. Note that trees that mix the species found in the granddaughters are not considered at all (i.e if granddaughter A is formed by two species and these appear separated in a pruned tree then this pruned tree will not be taken into account).

Note that, in contrast to bootstrap supports that are only informative on the support for a single partition, the phylome support value takes into consideration the specific arrangement between several partitions and it is thus more informative. Additionally it is to be noted that nodes that contain only two leaves will not be considered as they can not have any alternative distribution.